The 2012 election is over and in the books. A few very close races remain to be officially decided, but for the most part everything has settled down over the last week. By all accounts it was a very good night for the Democrats, with wins in the presidency, senate and state houses. They also performed better than expected in the House of Representatives. If we take the results as they stand now, the Democrats will have 202 seats v.s. the Republican’s 233 seats, a pick-up of 9 relative to the 2010 election. This got me thinking about how the Republicans could have maintained 54% of the house seats during a Democratic wave election.
Since I’m a statistician, the obvious answer was to go get the data and find out. Over the last few days, I was able to obtain unofficial vote counts for each congressional race except 3. The results from two unopposed Democrats in Massachusetts’ 1st and 2nd district, and one unopposed Republican from Kansas’ 1st district will not be available until the final canvas is done in December. Not including these districts 55,709,796 votes were cast for Democrats, v.s. 55,805,487 for Republicans, a difference of less than 100,000 votes.
Both of the candidates from Massachusetts also ran unopposed in 2008, where they garnered 234,369 and 227,619 votes respectively, which seems like a good estimate for what we can expect this year. In 2008 Kansas’ 1st district had a total of 262,027 votes cast. We will assign all of them to the Republican candidate as an (over) estimate, as the old 2002 district lines are similar to their 2012 placements. Using these numbers we get estimated vote counts of 56,171,784 for the Democrats and 56,067,514 for the Republicans, leading to a 100,000 vote advantage for the Democrats. Either way, this election was a real squeaker in terms of popular vote, which in percentage terms is 50.046% to 49.954%. Until the full official results are released, I would classify this as “too close to call,” but find a Democrat popular vote victory likely.
Nate Silver recently looked at the differences in the number of votes cast in 2008 v.s. those already reported in 2012, and found that California has reported 3.4 million fewer votes this election than 2008, suggesting that millions of mail-in ballots remain waiting to be certified. Somewhat similarly, New York reported 1.5 million fewer votes, though this may be due (at least in part) to the effects of hurricane Sandy. These were the only two states with differences > 1 million, and they both lean heavily Democratic, which may well push the popular vote totals for the Democrats into “clear winner” territory.
In a certain sense, the winner of the popular vote is irrelevant, as the only thing that matters in terms of power is the number of seats held by a party. But if the Democrats win, then they can reasonably claim that they (even as the minority party) are the ones with the mandate to enact their agenda.
Even though the popular vote is razor close in the current unofficial results, the distribution of seats is certainly not. We shouldn’t expect there to be a perfect correspondence between the popular vote and seats, because who wins the seats depends on how the population is divided up into congressional districts. As a simplified example consider three districts, each with 100,000 voters. District 1 is heavily Democratic, with 100% of votes going to the democratic candidate, while districts 2 and 3 are swing districts where 51% of the vote goes to the Republicans. In this simplified example, the Democrats would win nearly 2/3 of the popular vote, but only 1/3 of the seats.
So, if we expect there to be a discrepancy between popular vote and seat totals, the question then becomes: Is this election unusual? To answer this, we can look at the official historical record going back to 1942 which gives us the following:
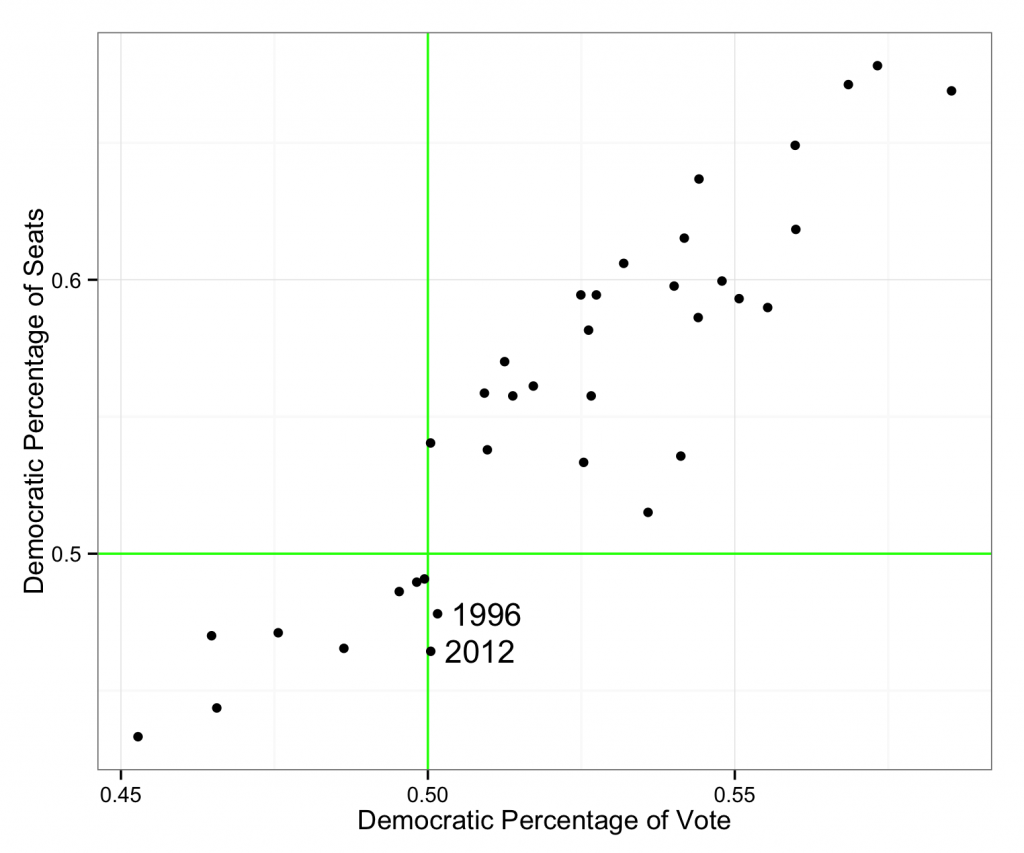
In almost every election in the last 70 years, the party with the popular vote victory also won the majority of seats. The only exception to this was 1996, where the Democrats won the popular vote, but failed to attain a majority in congress. If 2012 turns out to be a popular vote victory for the Democrats, then their seat deficit would be unheard of in living memory. On the other hand, there was a very close election in 1950, where the Republicans lost by a margin of just 0.04%, but ended up with only 199 seats to the Democrats 234.
Redistricting, Gerrymandering, oh my!
Whether or not the official vote tally goes to the Democrats, the 2012 House of Representatives electoral landscape is unusual. The seat totals clearly favor the Republicans, but why? Some have noted that the congressional district lines were redrawn following the 2010 Census, a process that in many states is controlled by the state legislature, and that many of these lines seem to be constructed to maximize the political advantage of one party or the other. I was initially skeptical of these claims. After all, the two years most comparable to 2012 are 1996 and 1950, neither of which are particularly near a redistricting period. As is often the case, an examination of the data revealed evidence that was counter to my expectations.
First, let us explore how one would draw lines that maximize party advantage. Remember in our simple three district example, the advantage was gained by bunching all of the Democratic voters into one district, and maintaining slim advantages in the other two. So, the rule is to spread out your own vote into many districts, and consolidate your opponents voters into just a few. This can be a difficult geometric “problem” to solve, but an easy way to think about one possible route toward a solution is to focus on the swing districts. If a district is very close, you will want to alter its location so that it has just enough more Republican votes to make it a safe bet for your party. Ideally you will want to take these Republican votes from a safe Democratic district, making it even more Democratic. What you can then expect when you look at the distribution of districts is a clump of very safe Democratic districts, a clump of safe, but not overwhelmingly safe, Republican districts, and very few toss-up districts. This is what we call a bimodal distribution, and the process of redistricting with a focus on political gain is known as gerrymandering. There is nothing particularly Republican about it. Both political parties engage in gerrymandering, the difference being whether or not they control the redistricting process, and to what degree are they willing to contort the shape of their districts.
| Authority to draw lines | # of Congressional districts |
| Democratic party | 44 |
| Republican party | 174 |
| Split between parties | 83 |
| Independent Commission | 88 |
| Only one district in the state | 7 |
| Non-partisan legislature | 3 |
| Temporary court drawn | 36 |
The Republican party was in control of the redistricting of 174 districts, v.s. just 44 for the Democrats. Just to give a specific example, Ohio had a Republican controlled redistricting process, which though wildly successful for Republicans, lead to torturously shaped districts. Republicans won 52.5% of the vote in Ohio, but obtained a staggering 75% of the seats.
But that is just one state, what about the rest of the districts? If we plot the proportion of people in each district that go to the Democrats, broken down by who was in control of redistricting we see clear evidence of clumping into safe, but not overwhelmingly safe territory for the redistricting party.
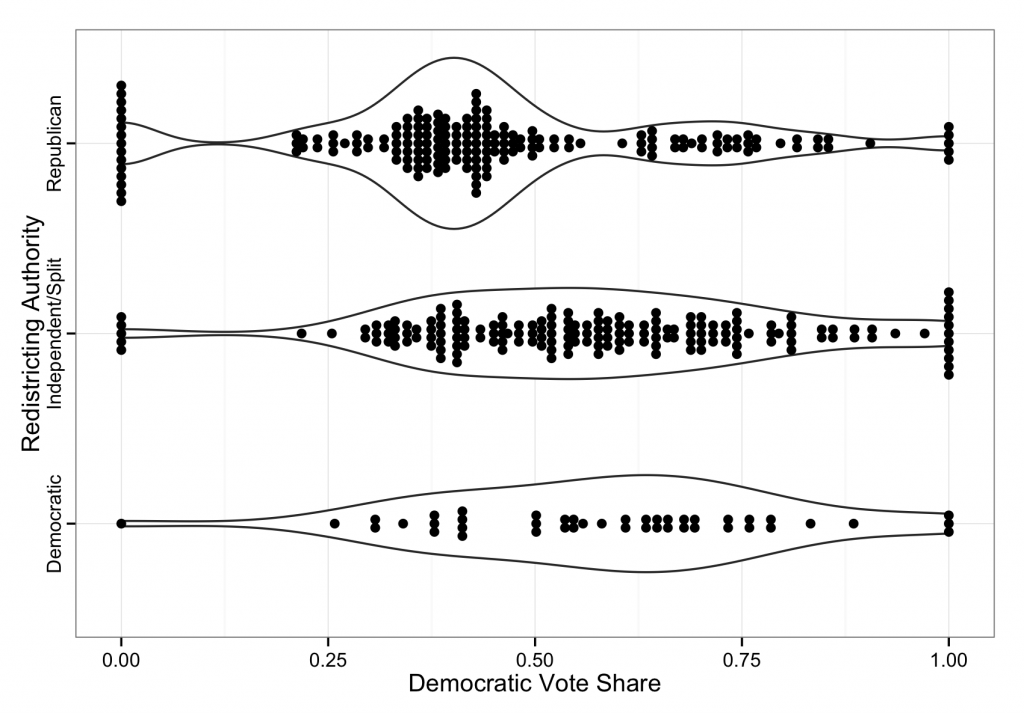
The way to read this plot is that each point represents a district, with its position being the proportion of people in the district who voted for the Democratic candidate. The lines represent a smoothed estimate of the distribution, with wider parts indicating increased density. Among the districts where Republicans had control, we see a characteristic bimodal distribution, with many districts chosen to be relatively safe Republican strongholds, with a smaller group of heavily Democratic districts. The same trend may be present in the Democratically controlled districts, but there are too few of them to see the trend clearly. Alternatively, in districts where the decision making is split between parties, or delegated to an independent group, we see a more natural distribution of vote shares, with a good number of toss-up districts.
But can we prove that it swung the election?
To parse out the effect of redistricting on the election results in a non-descriptive sense, it is necessary to construct (a simple idealized) model of how redistricting affects the probability of winning a district. To do this, we assume that the probability of winning a district within a state is related to the partisanship of the state (i.e. we expect a higher proportion of Republican seats in Alabama as compared to New York), which we will measure by the share of the vote that Romney won in the state. Second, control of redistricting (either Democratic, Republican, or Independent/Split) yields an increase (or decrease) in the odds of a win. We slap these two together into a standard statistical model known as a logistic regression, which yields the following:
| Variable | Df | Chi-squared | p-value |
| Romney vote | 1 | 31.4 | <0.001 |
| Redistricting control | 2 | 9.1 | 0.010 |
| Residuals | 385 |
This table tells us two important things through its p-values. With p-values, the closer to 0, the more significant the relationship. First, that the partisanship of a district matters, because the proportion voting for Romney is very significantly related to the probability of congressional control. Secondly, control of redistricting matters. If the redistricting process were fair, we would see the magnitude of the trends that we see in this data only once every thousand years (10 years between redistricting / 0.010 ). This gives us a high degree of confidence that political concerns are the driving force in redistricting when politicians are put in charge of it (shocking, I know).
This effect is relatively large. Consider an idealized swing state, where Romney won exactly 50% of the vote. Our model estimates the proportion of the congressional delegation who are Democrats as:
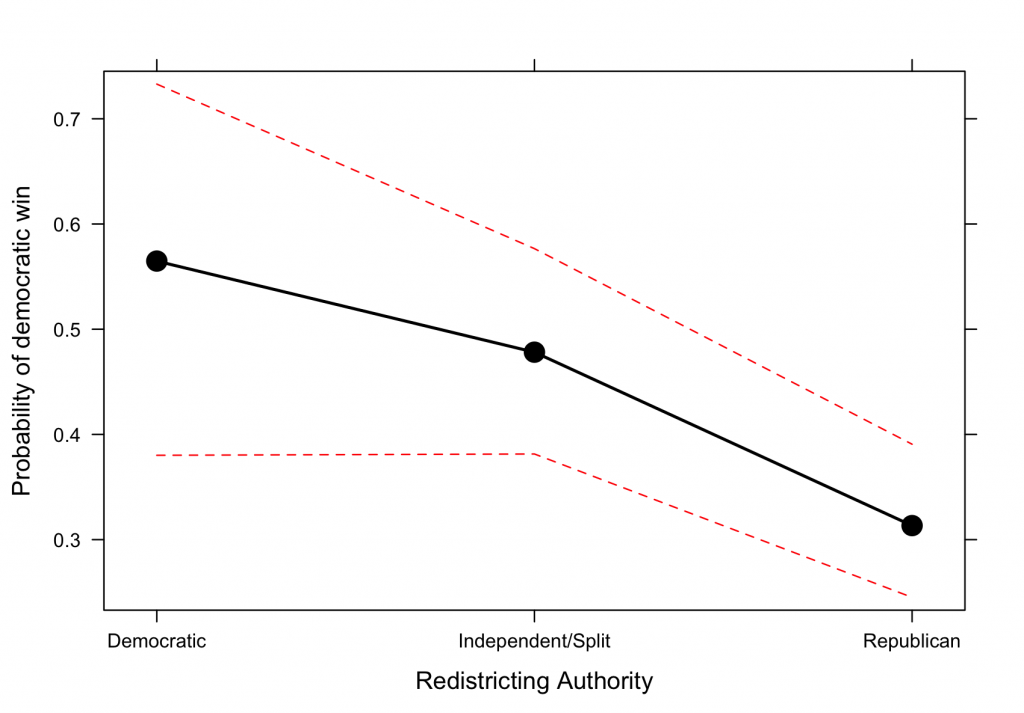
Here the model estimates that districts from an independent/split source are roughly unbiased with an estimated proportion of seats of 48%. If the Republicans control the process then we would expect only 31% of the delegation to be Democrats. This is slightly above what we observed in Ohio, where only 25% of the delegation were Democrats, despite Romney’s percentage of the vote being nearly 50%. With the Democrats in control we see a smaller bias than the Republicans with an estimated 56% belonging to the Democratic party, but our confidence in this estimate (denoted by the red dotted lines) is small due to the small number of redistricting opportunities that they had.
A perfect world
What would have happened if the entire redistricting process was controlled by independent or bipartisan agreement? Well, our simple model can tell us something about that. By counterfactually assuming that all redistricting was done independently or by split legislature, it estimates that the proportion of Democrats in the current congress would be, on average, 52%. If Democrats got to pick all the lines it would be 59%, and under complete Republican control it would be just 37%.
Conclusions
So what lessons can we take away from this analysis? Control of the redistricting process is a powerful tool for those who would use it as a tool. The model estimates that who controls the process could yield 17% point swings (56%-39%) in a typical swing state. This is consistent both with the results from the general election as a whole, and Ohio in particular. While I would love to see the implementation of an algorithmic solution to the problem of district formation (if only to hear the pundits trying to say minimum isoperimetric quotient), it appears that independent commissions, or even bipartisan agreement within a legislative body are sufficient to have fair lines. As of now, 6 states decide their districts based on an independent commission, and it is hard to think of an honest argument why every state should not adopt this model. Economics teaches us that incentives matter, and if you give politicians the incentive to bias districts in their favor, it is a safe bet that they will do so.
————————————–
Fellows Statistics provides experienced, professional statistical advice and analysis for the corporate and academic worlds.